If you allow me a momentary tangent, the work we’ve done on Pokémon will become much more clear. Our lab’s expertise predominantly deals with absolutely tiny blobs of stuff which we have helpfully dubbed “reverse micelles”. It’s a straight-forward and utilitarian name. Micelles consist of amphiphilic molecules known as surfactants which separate a non-polar (oily) interior from an aqueous (water) exterior, collectively comprising a single phase. Most people are familiar with micelles as hand and dish soap. Our micellar solutions are called “reverse” because we flipped the whole thing inside out so that we have water held on the inside, and the whole bubble ensemble held in a non-polar phase of usually isooctane. Micelles were obviously named before they were aware that you could flip them inside out, although I do acknowledge how confusing it could be for people who didn’t know about right-side-in micelles first.
Our micelles use a surfactant known as Aerosol-OT, or AOT for short. Chemically, it is better identified as bis(2-ethylhexyl) sulfosuccinate and AOT is just a trade name; but AOT seems to roll of the tongue much easier so lets stick with that. AOT is interesting because it produces reverse micelles which can be anywhere from 1 to 10 nanometers in diameter, which is exceedingly small. This means that the micelles are each about one million times smaller than a millimeter. To scale, it’s as if we were comparing a single centimeter to the entire circumference of the Earth. This type of system is very important because many important processes in plants, animals, and even you take place in spaces about the same size. So we use AOT reverse micelles as a model system to better understand how different things behave in such small spaces.
Recently, our work has begun to discover that AOT reverse micelles are not nearly as spherical as we assumed. Now scientists have actually known for decades that these reverse micelles weren’t perfectly spherical, but we thought they were at least close enough that we could model them that way. This may not actually be the case, which could have big impacts on how things behave inside of the reverse micelles (or rather, the things always behaved that way in the micelles, but the way we make sense of what’s happening could change dramatically). Because of this realization, we have started to develop the tools necessary to describe the shape of our reverse micelles.
Thank you for taking the time to read through that brief tangent and now is the part where we get back to Pokémon. Now that we have a few tools to describe shape, we put ourselves among the likes of Euclid, Plato, Al-Abbas ibn Said al-Jawhari, Kepler, Newton, and Gauss1, we began to ask the relevant questions. Questions like, “Do the evolutionary pressures of fire-type Pokémon influence their shape relative to ghost-type or normal-type Pokémon?” and “Is there a correlation between strength and shape among Pokémon?” As one is want to do.
Now that we’ve established the undeniable importance of our work, you’re probably asking yourself what we’re actually measuring. Well that’s simple. We are measuring:
- The eccentricity
- The convexity
- The curvature
Eccentricity
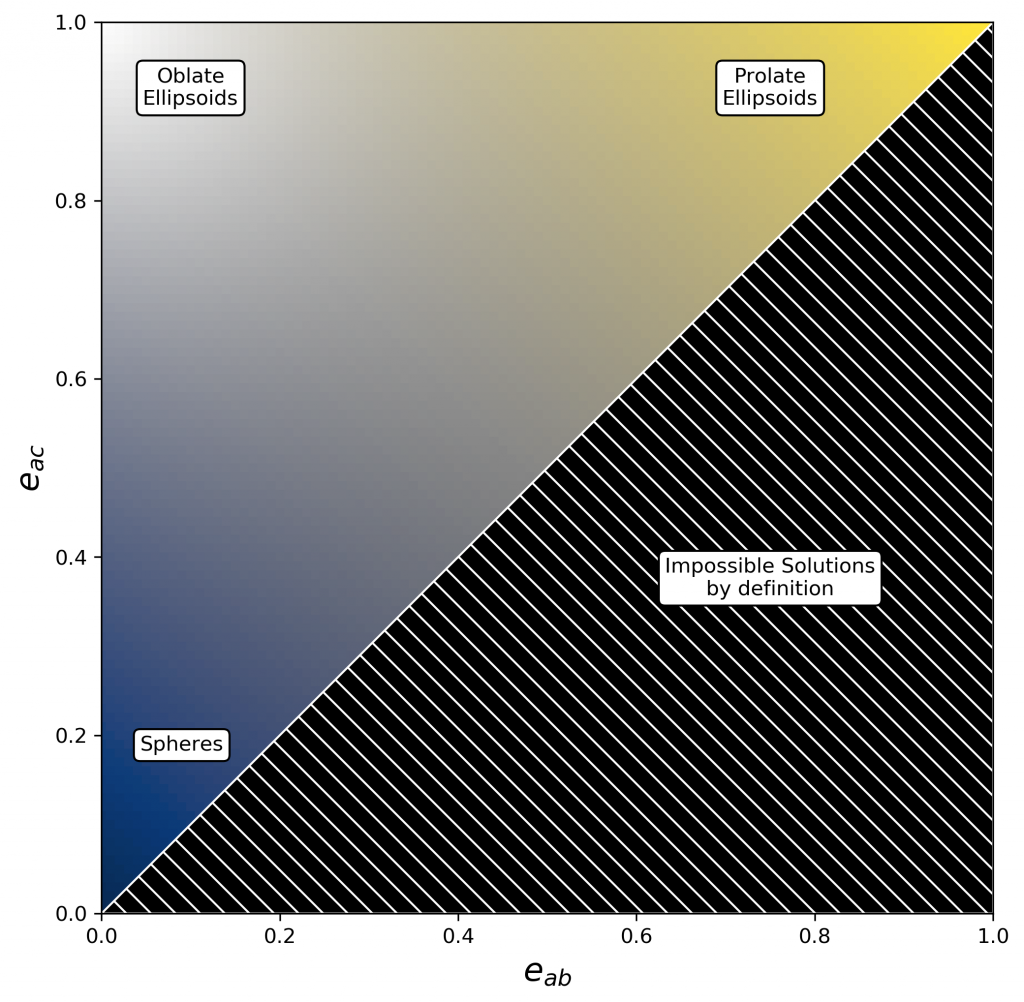
The eccentricity is a general measure of how mass is distributed about the figure. We do this by computing the moments of inertia for the Pokémon. We then diagonalize this matrix to obtain the principal moments of inertia (eigenvalues). We construct an ellipsoid with semi-axes such that if the ellipsoid had a uniform density, it would produce identical moments of inertia to the Pokémon. However, this is still not particularly useful since we are left with 151 different ellipsoids and no real way to compare them. We need hard numbers. In particular, there are 3 basic kinds of ellipsoids in existence and we would at least like to be able to group them into different classes. Those different kinds of ellipsoids are: spheres, prolate ellipsoids (cigar shaped objects), and oblate ellipsoids (disk shaped objects). This classification is where eccentricity actually comes in.
Eccentricity actually dates all the way back to Kepler and his study of the movements of planets and stars. Not everything orbited in a circle, and so he came up with the eccentricity to quantify how circular or non-circular a particular orbit was. But Kepler was working with planets and they trace a single path along some plane, so he only had an ellipse with two semi axes. We will call those semi-axes ![]() and
and ![]() (and since the naming of them is arbitrary, we’ll say
(and since the naming of them is arbitrary, we’ll say ![]() just to keep things straight). In this case, eccentricity,
just to keep things straight). In this case, eccentricity, ![]() , is defined as
, is defined as
(1) ![]()
But the ellipsoids we are generating to model the Pokémon have 3 semi-axes and are, in fact, 3D objects. This complicates things a bit since the equation for eccentricity compares only two semi-axes. If we used this equation on the Pokémon, we could use something like the biggest semi-axis, ![]() , and the smallest,
, and the smallest, ![]() , and learn if the Pokémon is spherical or not. This might work well if all we cared about was “Is this Voltorb or Electrode?” but doesn’t help us in any other circumstance. We need information about that middle semi-axis,
, and learn if the Pokémon is spherical or not. This might work well if all we cared about was “Is this Voltorb or Electrode?” but doesn’t help us in any other circumstance. We need information about that middle semi-axis, ![]() , in order to differentiate which type of ellipsoid best models each Pokémon. To do so, we use a coordinate pair of eccentricity values,
, in order to differentiate which type of ellipsoid best models each Pokémon. To do so, we use a coordinate pair of eccentricity values, ![]() and
and ![]() . Just like you might expect, they are defined as
. Just like you might expect, they are defined as
(2) 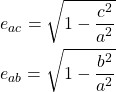
And just to give you an idea of what this looks like on a plot, I direct your attention to this very pretty graph below (if we do say so ourselves).
Convexity
The next measure we use is called “convexity”, but this probably doesn’t mean much to the average person. You might vaguely remember “convex” as being a word that means something in geometry, and would therefore reason that “convexity” is a measure of how convex something is. If you thought so, congratulations! You were exactly correct and deserve a cookie. Let’s start with the idea of a simple polygon. A convex polygon is one in which any line segment drawn between any two points on the boundary is entirely contained within the polygon. Go ahead and check that with your standard square or triangle and it’s easy to verify that these are convex polygons. So then what isn’t convex? For this, picture a star. You can easily pick two points of the star and notice that everything except the endpoints is outside of the star, and therefore a star is not convex. Incidentally, you can do the same thing with yourself. Draw a line between any two of your fingers and you will notice that the line is outside of your body. Therefore you are not convex, and the old saying is mathematically proven to be true: the stars really are just like us.
Convexity endeavors to put a number on this idea. There are a few different definitions, but we can make some basic assumptions to simplify things. For example, geometers will point out that it is theoretically possible to create a shape with an infinitely thin spike coming out of it. If you do this, then many definitions of convexity, such as the one we plan to use, will fail. However, as reasonable people of the world, we would like to ask, when was the last time you saw an infinitely thin spike in the real world? And thankfully, Pokémon are equally finite and real and so we can use one of the simpler definitions. Namely, we’ll define convexity as
(3) ![]()
Where ![]() is the shape or object we are measuring the convexity of,
is the shape or object we are measuring the convexity of, ![]() is the convexity of the shape (that’s the Greek capital letter “Xi”, by the way),
is the convexity of the shape (that’s the Greek capital letter “Xi”, by the way), ![]() represents the volume of whatever is in parantheses, and
represents the volume of whatever is in parantheses, and ![]() is the convex hull of the object. Now the convex hull is a new idea, but it’s really quite simple. It is the smallest possible shape which is completely convex and contains the shape you are analyzing. Let’s think back to the star. If we draw a line between any two points, we can prove that the star is not convex. However, if we draw a line between every two consecutive peaks, then we will have drawn a pentagon (if you drew a 5 pointed star, at least. I trust you can extend this argument to other types of stars if you chose to be creative). And not just any pentagon, but the smallest pentagon which also contains the star. That pentagon is the convex hull of the star. So to measure convexity, we simply divide the volume of the object by the volume of the convex hull of the object. If the object is completely convex, then it is it’s own convex hull and you get a convexity of one. And every time you have less volume in your shape than in the convex hull, the convexity drops a little bit.
is the convex hull of the object. Now the convex hull is a new idea, but it’s really quite simple. It is the smallest possible shape which is completely convex and contains the shape you are analyzing. Let’s think back to the star. If we draw a line between any two points, we can prove that the star is not convex. However, if we draw a line between every two consecutive peaks, then we will have drawn a pentagon (if you drew a 5 pointed star, at least. I trust you can extend this argument to other types of stars if you chose to be creative). And not just any pentagon, but the smallest pentagon which also contains the star. That pentagon is the convex hull of the star. So to measure convexity, we simply divide the volume of the object by the volume of the convex hull of the object. If the object is completely convex, then it is it’s own convex hull and you get a convexity of one. And every time you have less volume in your shape than in the convex hull, the convexity drops a little bit.
Curvature
The last measure we look at is the curvature of the Pokémon. Curvature is really quite a simple thing. You might have learned about it in calculus, if you weren’t too busy playing through the Final Four, of course (don’t worry. We fully support your choices). Imagine that we have some arbitrary curve, which is a fancy way of saying draw some random squiggly line on a piece of paper. Take any point on that squiggly curve and imagine drawing a circle that best approximates the curve at that point. A shallow curve will require a very large circle to approximate it while a very narrow and sharp curve will need a very small circle to approximate it. The technical name for that circle is called an “osculating circle” and there’s a very simple relationship between the radius of this osculating circle and curvature:
(4) ![]()
where ![]() is the curvature and
is the curvature and ![]() is the radius of that osculating circle. And so it’s easy to see that the very narrow, sharp bend in your curve, which has a very small radius for the osculating circle, has a very high curvature. This should make sense. The curve is curving quite a bit, and so we say it has high curvature (are you sensing the pattern?). Try think about it as if you’re driving. If you take a very gentle turn on a relatively straight highway, you don’t have to move the wheel all that much, the road isn’t curving all that much. This bend has very low curvature. On the other hand, if you pull a U-turn, and please follow all applicable laws in your area when doing so, you have to turn the wheel quite a bit, you are literally moving through a full 180 degrees of movement, and this turn would have a very high curvature.
is the radius of that osculating circle. And so it’s easy to see that the very narrow, sharp bend in your curve, which has a very small radius for the osculating circle, has a very high curvature. This should make sense. The curve is curving quite a bit, and so we say it has high curvature (are you sensing the pattern?). Try think about it as if you’re driving. If you take a very gentle turn on a relatively straight highway, you don’t have to move the wheel all that much, the road isn’t curving all that much. This bend has very low curvature. On the other hand, if you pull a U-turn, and please follow all applicable laws in your area when doing so, you have to turn the wheel quite a bit, you are literally moving through a full 180 degrees of movement, and this turn would have a very high curvature.
In three dimensions, this same principal applies. The only difference is that there’s now more than one direction we could measure curvature in. We could measure curvature along the x-axis, or the y-axis, or the z-axis, or even just some random line we decide to draw. For our purposes, we handle this very simply: we just take the average of the curvatures in each direction.
Conclusions
Now that you understand what these numbers mean and what you are looking at, we hope that the analyses we’ve performed on Pokémon will make more sense to you!
